ИНФОРМАЦИЯ И ЕЕ КОДИРОВАНИЕ
|
 |
Задача 1.
Задано сообщение из 50 символов на алфавите из 5 букв. Напишите
программу, которая вычисляет вероятности каждого символа и по формуле
Шеннона определяет среднюю информацию, приходящуюся на 1 символ,
и общую информацию в сообщении. Убедитесь в том, что: 1) если все
символы одинаковы, информативность сообщения минимальна; 2) если
символы алфавита встречаются с равными вероятностями, то сообщение
несет максимальное количество информации.
|
В программе ПР-1 из сообщения r="aqws...ea" вырезается
первый, второй, третий и последующие символы, определяется
частота (эмпирическая вероятность) каждой буквы алфавита,
результат выводится на экран. Для нахождения средней информации,
приходящейся на 1 символ, используется формула Шеннона:
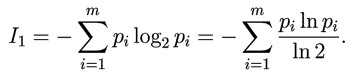
| 
|
Чтобы определить информативность всего сообщения, необходимо
получившуюся величину умножить на число символов N. Если
какая-либо буква ни разу не встречается в тексте, то ее
эмпирическая вероятность равна 0, логарифм не определен.
Чтобы избежать этого, вместо ln(pa) в программе вычисляется
ln(pa+0.001). С помощью программы можно убедиться в том, что
информативность сообщения максимальна тогда, когда все символы
используются с равными вероятностями. Если в сообщении повторяется
один и тот же символ, то информативность сообщения равна 0.
Программа ПР-1.

 |
Задача 2.
Напишите программу, кодирующую двоичным кодом сообщение из
20 букв на алфавите из 8 букв. На каждую букву приходится три
двоичных разряда: a - 000, b - 001, c - 010, ... , h - 111.
На экран выводится закодированное сообщение, затем осуществляется
декодирование.
|
Используется программа ПР-2. Из заданного сообщения s="abc..defa"
вырезается по одному символу, он кодируется тремя битами и записывается
в стринговую переменную b. Аналогичным образом осуществляется
декодирование.
| 
|
Программа ПР-2.

 |
Задача 3.
Имеется сообщение 01101 ... 01. Напишите программу, кодирующую
его помехоустойчивым кодом, в котором каждый бит утраивается,
затем вносит ошибки с заданной вероятностью p и декодирует
сообщение.
|
Используется программа ПР-3. Из заданного сообщения aa1="01101 ... 01"
вырезается по одному символу 0 или 1, он утраивается, то есть получается
000 или 111. Результат выводится на экран.
После этого в получившееся закодированное сообщение с заданной
вероятностью вносятся ошибки, сообщение выводится на экран.
Затем оно декодируется в соответствии с правилом: кодовые
последовательности 111, 011, 101, 110 воспринимаются как 1, а
кодовые последовательности 000, 100, 010, 001 воспринимаются как 0.
Данный код исправляет часть ошибок. Программа вычисляет относительное
число ошибок при заданной вероятности p и позволяет изучить k
от p и построить график.
| 
|
Программа ПР-3.


| Задача 4.
Имеется сообщение 01101 ... 01. Напишите программу, которая
разбивает его на кадры по 7 бит и добавляет восьмой бит четности.
|
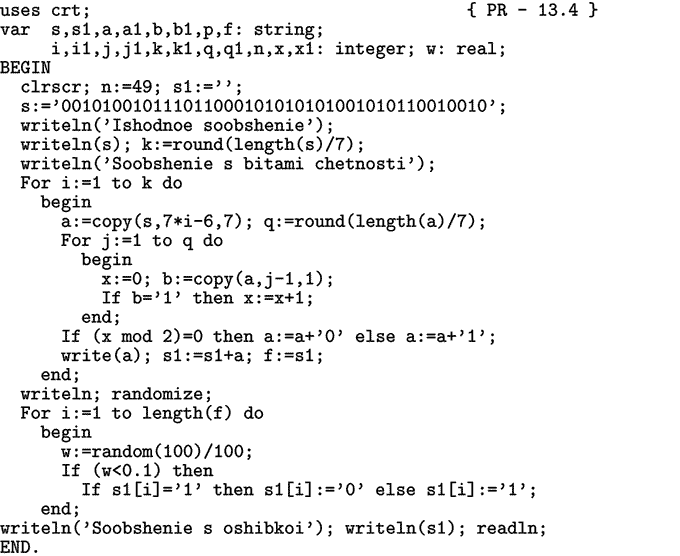
Программа ПР-4 содержит цикл, в котором вырезаются по 7
бит и в них определяется количество единиц. Если число единиц
нечетно, то добавляется восьмой бит четности 1, а если четно -
то 1. Результат выводится на экран, затем в сообщение добавляются
ошибки, случайным образом инвертируются некоторые биты.
| 
|
Программа ПР-4.
Тексты программ находятся в zip-архиве,
файл gl-13.pas.
ВВЕРХ
Майер, Р. В. Задачи, алгоритмы, программы / Р. В. Майер [Электронный ресурс].
- Глазов: ГГПИ, 2012 //
Web-site http://maier-rv.glazov.net .
|