Многочисленные эксперименты подтвердили ограниченность концепции механического детерминизма и убедительно показали, что даже простые механические системы в некоторых случаях ведут себя непредсказуемым образом. Возникшая теория детерминированного хаоса исследует нерегулярные движения физических систем, которые удобно изучать, используя метод компьютерного моделирования. При этом могут быть рассмотрены основные понятия хаотического движения: неустойчивость, перемешиваемость и т.д.
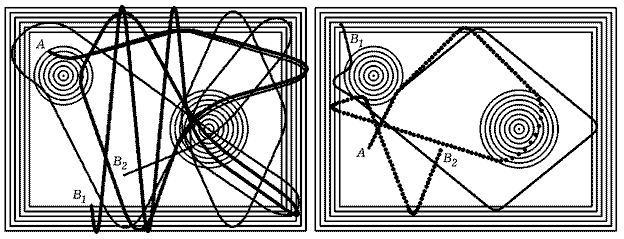
1. Неустойчивость систем к изменению их параметров, начальных условий, внешних воздействий может быть продемонстрирована на примере бильярда с наклонными стенками, поверхность которого имеет конические выступы и углубления (Программа 1). Если из точки A запустить два шарика, скорости которых незначительно отличаются, то через некоторое время они окажутся в далеко отстоящих точках B1 и B2.
Uses dos, crt, graph; Программа 1 (Pascal)
Const dt=0.01; time=55000;
Var m, Fx, Fy, x, y, vx, vy, xx, yy, x1, y1, x2, y2 : real;
Gd,Gm, i, j, t : integer; ax, ay, F, F1, F2, l1, l2 : real;
BEGIN Gd:=Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
If GraphResult <> grOk then Halt(1);
x1:=130; y1:=150; x2:=430; y2:=260;
rectangle(60,60,580,420);
circle(round(x1),round(y1),60);
circle(round(x2),round(y2),80);
m:=0.1; x:=120; y:=300; vx:=20; vy:=-40;
Repeat t:=t+1; Fx:=0; Fy:=0; F1:=0; F2:=0;
l1:=sqrt(sqr(x1-x)+sqr(y1-y));
l2:=sqrt(sqr(x2-x)+sqr(y2-y));
If l1<60 then F1:=-6; If l2<80 then F2:=8;
If x<60 then Fx:=6; If x>580 then Fx:=-6;
If y<60 then Fy:=6; If y>420 then Fy:=-6;
Fx:=Fx+F1*(x1-x)/l1+F2*(x2-x)/l2;
Fy:=Fy+F1*(y1-y)/l1+F2*(y2-y)/l2;
ax:=Fx/m; ay:=Fy/m; xx:=x; yy:=y;
vx:=vx+ax*dt; vy:=vy+ay*dt;
x:=x+vx*dt; y:=y+vy*dt;
{circle(50+round(0.8*x),240-round(2*vx),1);}
If round(t/20)*20=t then circle(round(x),round(y),1);
delay(50);
until (t>time)or(KeyPressed);
Repeat until KeyPressed; CloseGraph;
END.
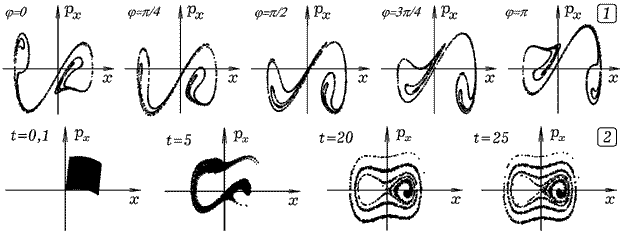
2. Проявлением хаотичности движения системы является фрактальная структура сечения Пуанкаре. Программа 2 позволяет получить сечения Пуанкаре для маятника Дафинга, представляющего собой частицу, колеблющуюся в поле с потенциалом (рис.2.1).
Uses crt, graph; Программа 2 (язык Pascal)
Const m = 1; k = 4; r = 0.5; w = 2.3;
dt = 0.002; pi = 3.1415926;
Var Gd, Gm : integer; f, t, x, v, a, z, zz : real;
BEGIN Gd := Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
If GraphResult <> grOk then Halt(1);
line(200,0,200,480); line(0,280,640,280); x:= 0; v:= 0;
Repeat t:= t + dt; f:=1*sin(w*t);
a:=(f-k*(x*x*x-x)-r*v)/m; v:=v+a*dt;
x:=x+v*dt; z:=sin(w*t+3*pi/4);
If (z>0)and(zz<0) then circle(round(100*x) + 200,
280 - round(100*v),1); zz:= z;
until (t>10000); Repeat until KeyPressed; CloseGraph;
END.
3. Необходимым и достаточным условием хаотического движения является перемешиваемость фазового пространства (ФП). Под этим понимают сильное изменение формы ячейки ФП, соответствующей движению ансамбля систем, при котором ячейка как бы однородно перемешивается во всем ФП. Она превращается в тонкую паутинку, нити которой пронизывают все ФП, при этом сохраняя свой объем. Программа 3 моделирует колебания ансамбля маятников Дафинга, отличающихся начальными условиями, и позволяет показать эволюцию соответствующего им фазового объема (рис. 2.2).
Uses crt, graph; Программа 3 (Pascal)
Const m= 1; k = 4; dt = 0.002; pi = 3.1415926;
Var i, j, Gd, Gm: integer; v, a, f, t, x : real;
BEGIN Gd := Detect; InitGraph(Gd, Gm, 'c:\bp\bgi');
If GraphResult <> grOk then Halt(1);
line(200,0,200,480); line(0,280,640,280);
For i:=1 to 40 do For j:=1 to 40 do begin
x:=0.04*i; v:=0.04*j; t:=0;
Repeat t:=t+dt; a:=-(x*x*x-x)/m;
v:=v+a*dt; x:=x+v*dt;
until t>20;
circle(round(50*x)+200,280-round(50*v),1); end;
ReadKey; CloseGraph;
END.
Литература:
1. Заславский Г.М., Сагдеев Р.З. Введение в нелинейную физику: От маятника до турбулентности и хаоса. -- М.: Наука, 1988. -- 368 с. 2. Электронный ресурс: http://maier-rv.glazov.net. Майер Р.В. Изучение хаотического движения с помощью компьютерных моделей // Научное обозрение. --- 2008. --- N 1. --- 63 -- 65 с. ВВЕРХ
|